
Arrays or bar models? What about number lines? We can – and do - get geeky and passionate about every area of mathematics, but multiplication and division bring out our peak geekiness.
All the more so because, to celebrate a decade of bringing maths education research findings into primary classrooms across the UK, we treated ourselves to a collaborative project with our friends at Cambridge Maths – entirely focused on multiplication and division.
Working with them to map our curriculum sequencing against the Cambridge Maths Framework reignited some old passions – such as the fundamental importance of the array – and challenged our thinking. Would a reduced focus on bar models help children to shift from additive to multiplicative thinking? Were we making sufficient use of the number line?
An incredible 21-page report and access to the Cambridge Maths waypoints – as well as access to the research articles that have informed them – inspired us to delve back into our original research base.
We find ourselves with a renewed conviction as to the importance of the array model, and we’ve further developed our tasks and teacher modelling to support pupils’ flexibility with arrays.
As you probably know, an array is an arrangement of objects or pictures, in this case pictorial counters, into rows and columns. Here’s twelve as the product of three and four:
The power of the array is that we can still see four, three times (or three equal groups of four) but we can also clearly see three, four times (or four equal groups of three). The whole is always twelve.
While we often focus on the rows of an array, recognising the columns as equal groups is also important for pupils to develop flexibility in calculation and representation. Pupils should be able to recognise arrays in different orientations still show the same multiplication.
Recognising the different groupings presented in the same array leads pupils to the knowledge that three groups of four is the same as four groups of three and therefore that multiplication is commutative and supports them in developing a deeper understanding of the multiplicative structures, the relationship between multiplication and division thus, the fact families with four facts.
Towards the end of Year Two, our partner schools teach a two-week unit focused on multiplication and division. Teachers introduce pupils to two new facts to be shared about the one array involving fractions connected to division.
Here’s how we sequence the learning across the two weeks:
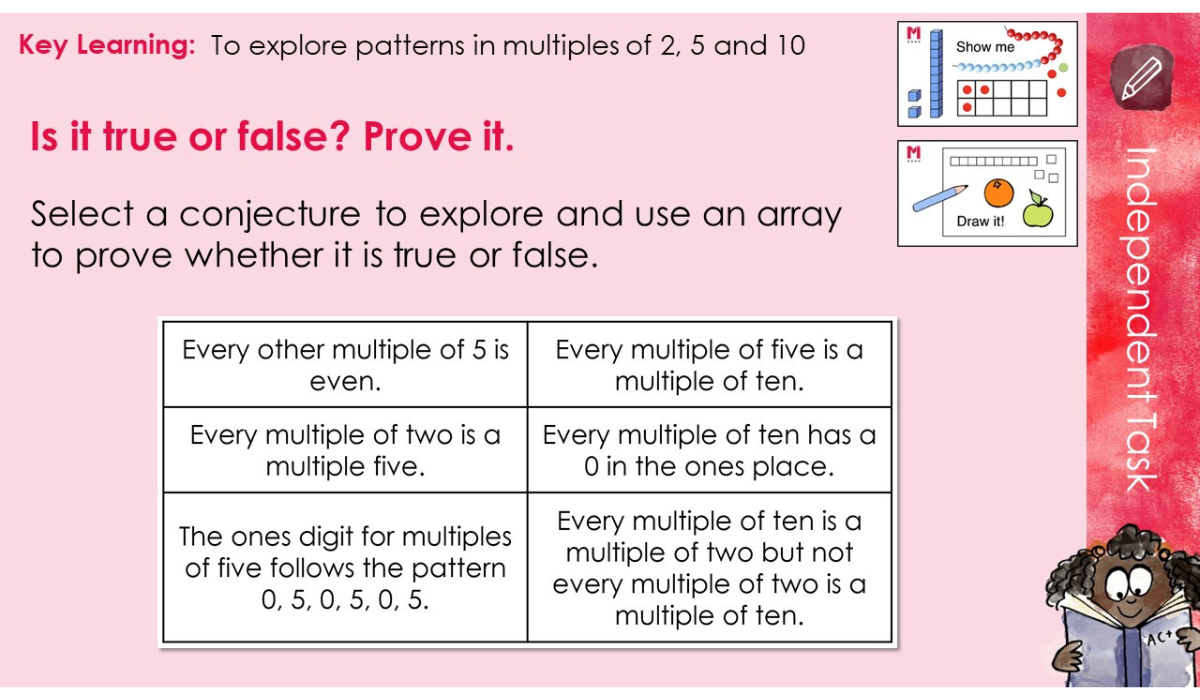
L1 Patterns in multiples (2, 5, 10)
Pupils draw on their knowledge of the 2, 5 and 10 times tables to explore multiples that appear across many times tables. Conjectures are explored and proven true or false using an array.
L2 Relationships between multiples of 2 and 4
Pupils begin by exploring and establishing that the ten times table is double the five times table before applying that knowledge to consider the relationship between the two times table and the four times table. They use arrays to prove and justify the relationship.
L3 Multiples of 2, 4, 5 and 10
Pupils consider whether a number could be a multiple of more than one times table before establishing what they know about multiples of 2, 4, 5 and 10, making conjectures as to whether it is or not using an array to prove it.

L4 Application of known facts (3x)
Pupils use arrays to represent a fact from the one times table and the two times table using this to derive a fact from the three times table. They then connect this to repeated addition on a number line.
L5 Consolidation lesson
We always build flex into our curriculum sequencing, so that teachers can teach responsively. This lesson – and lesson 10 – are to be used flexibly at an appropriate point in the unit.
L6 Fact Families (1)
Pupils explore the commutative property of multiplication. They derive division facts from known multiplication facts.
L7 Fact Families (2)
Pupils build on their learning from the previous lesson and bring in their fractional knowledge to describe an array, creating six facts for the one array.

L8 Inverse relationships
Pupils return to contexts where all values are known and explore representing it articulating whether it is a multiplication or division context. Pupils then consider whether an array can be used to articulate both a multiplication and a division structure.
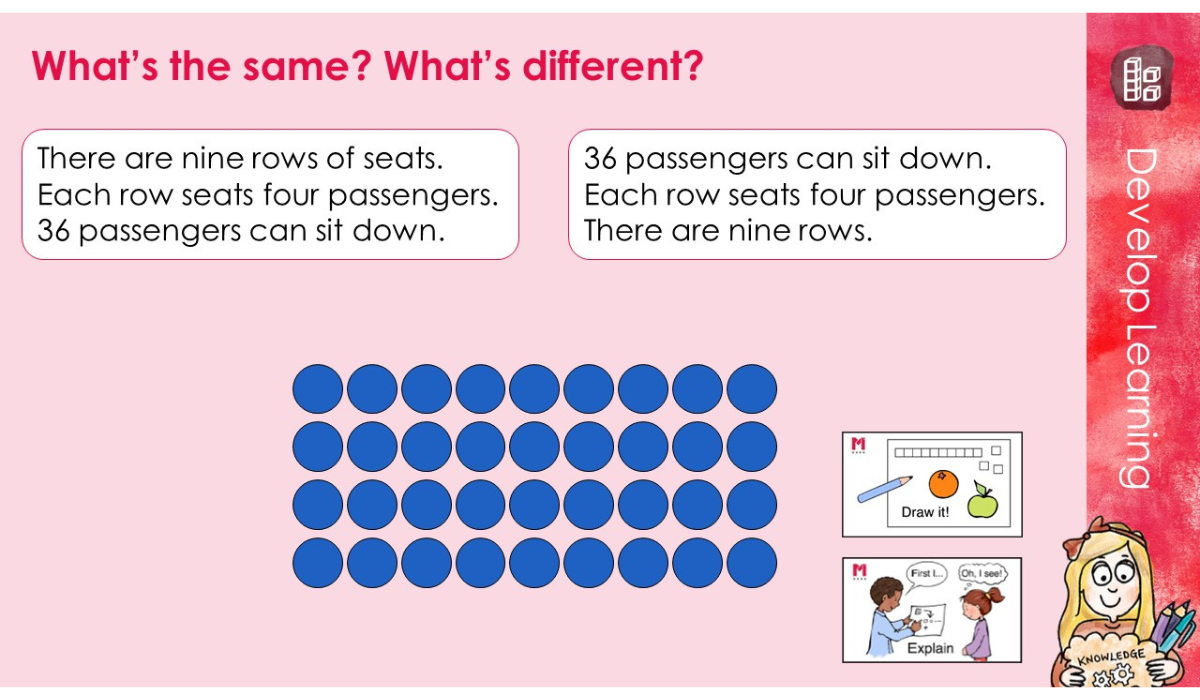
L9 Multiplicative relationships
Pupils build on their knowledge from the previous lesson to solve missing number equations drawing on their knowledge that multiplication is the inverse of division and vice versa.
L10 Consolidation lesson
We always build flex into our curriculum sequencing, so that teachers can teach responsively. This lesson – and lesson 5 – are to be used flexibly at an appropriate point in the unit.
‘Fave four’ – a few of our favourite pieces of research into multiplication and division
“I was good at my times tables when I was nine, now I can’t remember them”: Learning multiplication facts with conceptual understanding. – Richard Harvey Swanston (ATM) 2017
The array representation and primary children’s understanding and reasoning in multiplication – Barmby, Harries, Higgins and Suggate (Educational Studies in Mathematics) 2009
Young children’s understanding of division: The relationship between division terms in a noncomputational task. – Correa, Bryant and Nunes (Journal of Educational Psychology) 1998
Awareness of pattern and structure in early mathematical development. – Mulligan and Mitchelmore (Mathematics Education Research Journal) 2009